Difference between revisions of "3-dimensional pipe bending"
m (tinker) |
(→Explanation: Links) |
||
| Line 32: | Line 32: | ||
[[Image:Pipe_bend_3d.3.jpg|360px]] | [[Image:Pipe_bend_3d.3.jpg|360px]] | ||
| + | |||
| + | == See Also == | ||
| + | |||
| + | * [[Pipe bending|Pipe Bending]] | ||
| + | * [[The pipe bending spring|The Bending Spring]] (humour) | ||
[[Category:plumbing]] | [[Category:plumbing]] | ||
Latest revision as of 10:49, 14 January 2022
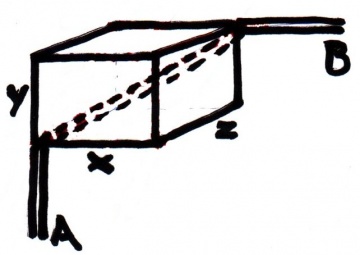
Pipe A is to be joined to pipe B. They run at right angles to each other but in different planes. A 135° coupling will be used on pipe B, so the problem is to bend pipe A to meet it at the correct angle. Like so:
- Measure the horizontal distance from the axis of pipe B to pipe A (i.e. if both pipes were longer, how far would they be apart horizontally?).
- Square this number (i.e. multiply it by itself) and then double it.
- Measure how far pipe B is above the point on pipe A where you would like to bend it.
- Square this number.
- Add it to the number you got in step 2.
- Take the square root of the number you got in the previous step (you can use a calculator for this).
- Fold or cut a piece of paper or card so that one side is the length you got in 6 and the other is the length from step 3. If these lengths are too long or short halve or double them (or scale them up up or down as needed, as long as you change them both equally).
- Bend pipe A to the angle of the diagonal across the template.
Explanation
Imagine a rectangular box linking the pipes so that the pipes are in line with edges of the box, and the coupling section between the pipes joins opposite corners of the box:
We know how far apart the pipes are (dimensions y and z) but dimension x is unknown.
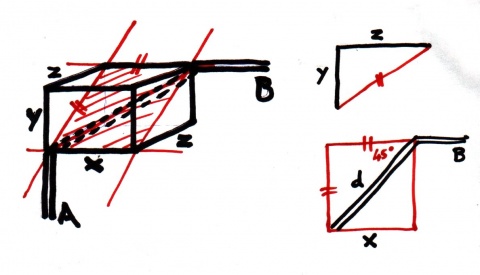
Now imagine the plane through the box from the edge which lines up with pipe B to the opposite edge. This plane cuts the sides of the box into triangles. We know the dimensions y and z of the triangle so by Pythagoras' theorem know the hypotenuse is sqrt(y2 + z2).
The plane intersects the box to make a rectangle (shown in red) and since the 135° coupling to pipe B lies in this plane it cuts the red rectangle to make an isosceles triangle so the sides marked (with two red ticks) are equal. Therefore the length of the hypotenuse (above) is equal to dimension x.
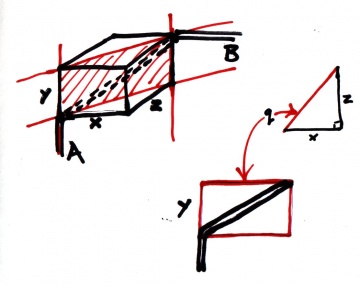
Lastly imagine the plane through the box from the edge which lines up with pipe A, to the opposite edge. This plane cuts the sides of the box into triangles with sides x and z from which we can calculate the hypotenuse, and makes the rectangle shown in red with sides y and sqrt(x2 + z2). Substituting for x gives
sqrt((y2 + z2) + z2)
= sqrt(y2 + 2*z2).
Folding or cutting a piece of paper or card to dimensions in the ratio of these two values gives a template for bending pipe A.
See Also
- Pipe Bending
- The Bending Spring (humour)