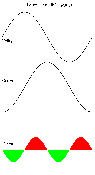Power factor
What is Power Factor
Some loads, eg electric heaters, have a power factor of 1. This means the current drawn is proportional to the voltage at any instantaneous moment, ie maximum current flows at voltage peaks of the mains supply.
So a 1kW heater on 240v consumes
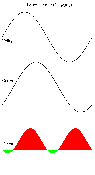
But some loads, such as Induction motors, behave a bit differently, having a power factor of less than 1. With a 0.8 PF motor, the current drawn lags behind the voltage by a tiny fraction of a second, so the peaks in current draw occur after the voltage peaks.
A 1kW motor with 0.8 pf on 240v draws
Notes:
- Power factor (PF) is a concept that only applies to electrical loads being powered from an AC supply. To try to apply it to a DC supply is meaningless.
- Domestic electricity users are only charged for that part of the current that produces real power, so in the motor example above the user only pays for 4.2A or 1kW, not 5.2A.
- It quantifies what proportion of the apparent power flowing into a load, is actually dissipated as real power.
Relevance to DIY
There are occasions where it may crop up in a DIY setting. The most common cases are when designing circuits, and when taking electrical measurements. In circuit design, a low power factor increases circuit current flow, and hence larger cable conductors sizes are needed. When attempting to measure current flow or voltage drop, a low power factor may result in incorrect readings, as it fools most test meters.
Its relevant to:
- Loads such as motors and LPF fluorescent lighting on circuits where their uncompensated current draw can exceed the circuit's design current.
- Tool use on generators
- Plug-in motorised appliances that can exceed 13A without Power Factor Correction (aka PFC, a number of measures designed to get a low power factor to look more like a higher one))
- Use of droppers
- Large lighting circuits using CFLs
- Sales blurb of dubious energy saving gadgets
- Industrial electricity use where users pay for uncorrected PF
- Knowing which type of fluorescent lighting ballast to buy
- Use of motors and other below 1 PF loads on invertors
Terminology
- PF
- Power factor
- PFC
- Power factor correction
- LPF
- Low power factor
- HPF
- High power factor
- W and kW
- Real power in watts and kilowatts
- VA and kVA
- Voltamps and kilovoltamps, voltage times current. Often greater than the real power consumed
Reactive power
With a DC supply, the power dissipated by a load is proportional to the voltage applied to it and the current through it (which is proportional to 1/ its resistance). The relationship between these is simple with DC.
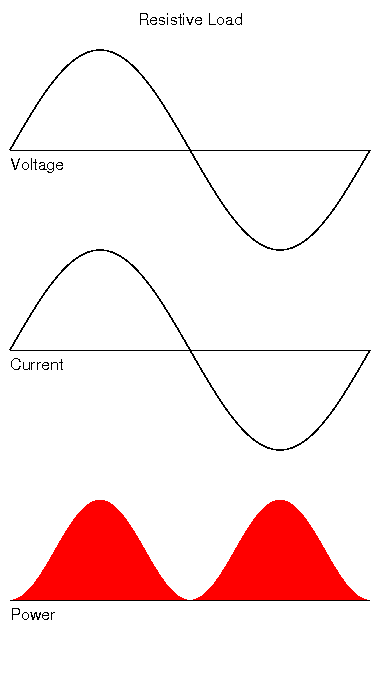
In the simplest cases, the same calculations also apply to loads being powered from an AC source (like the mains). A resistive load being driven from the mains, draws current in sympathy with the mains voltage; as V rises, the current rises, and as V falls current falls. At the zero voltage crossing point, current is also zero.
| Resistive load with AC supply | |
|---|---|
|
Here the image shows a short section of an AC supply plotted against time. The voltage goes through one complete cycle (of which there are 50 per second on UK mains). With a resistive load, the current flows back and forth through the load in exact synchronisation with the voltage. Many domestic appliances present this sort of load, including many heaters, filament lamps, and the type of electric motor commonly used in vacuum cleaners or similar appliances. Ohms law tells us that: Voltage = Current x Resistance or more commonly: V = IR we also know Power = Current x Voltage or W = IV So combining these we can also get: W = I x IR or W = I² R So if we know something about our load - say that it is rated at 100W at 230V, we can deduce from it that it must draw 100/230 or about 0.4A, and its internal resistance must equal 230/0.4 or about 575 ohms.
|
|
However things can get more complicated due to the effect of "reactive" elements in the load. These are typically components that have an inductance or capacitance. Inductors and capacitors actually store electrical energy (although in different ways). As you might imagine, having something that stores energy being fed from an AC supply, causes it to charge and discharge in response to the ever changing applied voltage. So during one part of the mains cycle its absorbing energy, and in another it gives the stored energy back again. Reactive elements in a load make the types of calculations that are easy to apply to simple resistive loads more complex.
Capacitive load
| Capacitive load with AC supply | |
|---|---|
|
By way of example, consider an extreme example: a load consisting of nothing but a capacitor being driven from an AC supply. Capacitors present an infinite resistance to a steady applied voltage, and lower reactance to quickly changing voltage. So with a sinusoidal input voltage, peak current is drawn when the voltage is at the zero point in the cycle, and the zero current is at the peak of the voltage cycle (i.e where the rate of change of voltage is zero). The effect is that the voltage and current waveforms still look the same, however they are no longer aligned (there is said to be a "phase shift" between them). Real measurable current is thus flowing into and out of the capacitor, but because it is being stored and returned rather than dissipated as heat, there is no real power being dissipated in the load.
Say we had a 5.5uF capacitor for a load, it reactance (i.e. AC resistance) is calculated using the formula: With a frequency of 50Hz we would get: So, from ohms law we can compute the current that will flow: 230/578 = 0.4A, but we also know that when the mains voltage is at its peak, the current is zero due to the phase shift, and when the voltage is zero, the current is 0.4A. If we were to work out the overall sum of Voltage x Current for a complete cycle of the mains, we get a total of zero. Hence we have the odd situation where the VA of the load (i.e the magnitude of the product of the current and voltage but ignoring the phase relationship) looks like 100, but the real power dissipated is actually 0W. As you can see from the power graph, power appears to both flow into the load (red section) and then half a mains cycle later, it flows out of the load. So on average, there is no power dissipated in the load at all. |
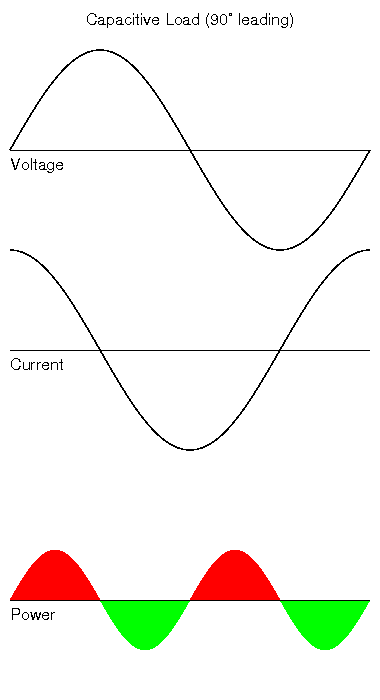
|
| |
Inductive load
A similar situation exists with an inductive load. Although inductors store energy, they do so in a magnetic field around a coil of wire, and thus behave differently to capacitors. (Since the wire is coiled, the magnetic field produced by the current flowing in the wire can also interact with adjacent coils.) As current flow through the coil changes, the associated magnetic field changes. This changing field induces a current flow in the wire. However the induced current flow caused by the changing field is in the opposite direction to the flow in the circuit. So the inductor tries to oppose changes in current flowing through it, by counteracting them using its stored energy. So inductors offer a low resistance path to stable voltages, but increase their resistance to changing ones - the opposite of a capacitor.
The main difference resulting from this is that the current waveform lags the voltage waveform rather than leads it. (see diagram to the right)
Real world inductors also have some resistance, so they always present a combined resistive and reactive load rather than a purely inductive load.
Switched mode supplies
Some electronic devices put the mains feed through a rectifier and to a reservoir capacitor. These loads draw a pulse of current at each mains voltage peak, and no current the rest of the cycle.
Generally anything that uses a switched mode supply (SMPSU) works this way. Prime examples are TVs, CFLs, computers, switched mode wallwarts and fluorescent lights that use an electronic ballast.
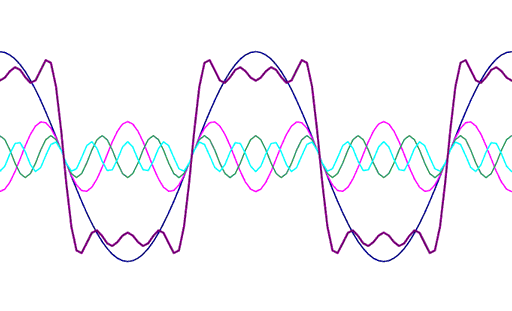
Recent EU legislation has stipulated that SMPS over 25W must now include PFC. However there's lots of legacy equipment in use without PFC.
The exact PF figures for such equipment without PFC varies a fair bit, and is often very low (this spice sim shows peak current draw about 8x rms current). The power drawn by such items is also usually low, so its not often an issue.
| A Switched Mode Power supply | |
|---|---|
|
Switched mode supplies are increasingly found in electronic appliances such as computer and electronic equipment, and also in energy saving light bulbs. Switched Mode Power Supplies (SMPS) typically rectify the mains and use this rectified AC to charge a capacitor. The capacitor is then in turn used to power the later parts of the power supply circuit. At each peak of the mains cycle the capacitor is "topped up", when the mains voltage is above the capacitor voltage, so current is only drawn near the peaks of the mains voltage. No current flows during the rest of the cycle. Unlike in the examples shown above, there is no phase shift visible between the voltage and current waveforms, the current waveform is distorted into a peaky square shape and is no longer the same shape as the voltage waveform. This change in shape also means that the current waveform is no longer made up from just a single frequency, but is in now made from a single fundamental frequency with a whole bunch of other frequencies mixed in with it. The following diagram shows how a single pure frequency will be distorted as you add in harmonic components: The blue line represents the main fundamental frequency. All the other smaller waveforms are harmonics (i.e. multiples of the fundamental frequency). If these are all added together, you get the resulting square looking purple wave. The more harmonic frequencies we add in, the cleaner looking the square wave becomes. The actual power dissipated by the load is no longer a simple product of Voltage and Current (since when dealing with AC, this calculation has the implicit assumption that the waveforms are both the same shape). As you can see from the power section of the graph, power is only dissipated in the PSU in short regular bursts. The PF of a computer SMPS is often be in the region of 0.7. Energy saving CFL ballasts can be as low as 0.1 |
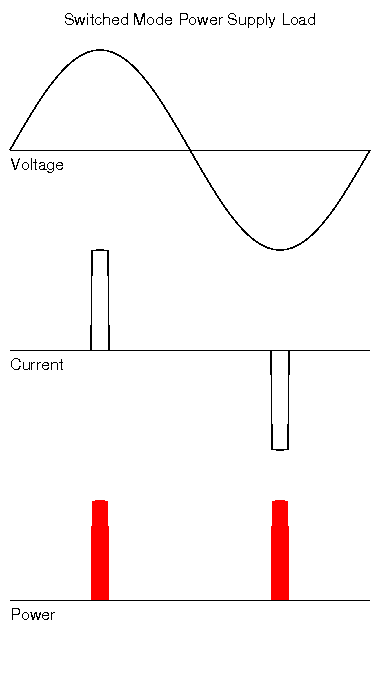
|
Dimmers
There are other causes of low power factor. One example is where current only flows in the load during some but not all of the mains cycle. giving rise to a non sinusoidal current waveform. No current flows until the triac fires.
Composite loads
In the real world, electrical loads are rarely just reactive, they are usually combined with a resistive element as well. This can give rise to the situation where there is a misalignment between the alternating voltage and the current drawn as before, but not as pronounced. If you look at the resulting power graph, you can see that in this example, most of the power flowing into the load is power transfer that is doing some useful work, but a small proportion is being returned as reactive power.
An appliance like an electric fan heater presents a load like this. The bulk of the current drawn supplies the resistive heater element. However a small amount powers the fan, typically an induction motor.
Other causes of low power factor
The above examples show the classical cause of non unity power factors. A typical real word example of a load that has a less than unity power factor as a result of these phase shift effects is an induction motor. Here a significant proportion of the current flow into the motor is actually reactive and does not get dissipated as work. A power factor of 0.5 is not be uncommon. Basic switchstart linear fluorescent lights are another common load with a low PF.
How is a power factor expressed?
A power factor is usually[1] expressed as a number between 0 and 1. A power factor of 1 (aka a "unity power factor") basically says the power in a load is like a resistive load, and ohms law applies. A PF of 0 is a completely reactive load, one that dissipates no real power at all.
The power factor of our load can be expressed as:
So in our capacitive and inductive examples above, the power factor
would actually be zero.
A load like this that is totally "reactive" would be unusual. In real world situations, loads can have both resistive and reactive components (and of those reactive components, the capacitive ones will have leading, and the inductive ones lagging phase shifts).
To compute the actual current flow into a load like this at any given time therefore requires vector arithmetic, ie taking into account not only the reactance of the leading and lagging components, but also the direction of their phase shifts.
[1] Note that this makes the assumption that power is always flowing in the traditional direction from source to load. In real world circumstances there are systems where on occasion power may flow in the reverse direction (e.g. a power distribution grid connected a property with a photo voltaic solar array). In some cases the nominal "load" becomes the supply. Practitioners working with these systems will therefore make reference to negative power factors in the range 0 to -1
Power factor correction
Often low power factor is correctable with power factor correction (PFC). While this is worthwhile in an industrial setting where customers are usually charged based on their VA loading rather than their real power loading in watts, its seldom useful in a domestic one where the meter reads actual power consumption regardless of the PF.
With poor PFs caused by current phase shifts, you can add a reactive component to the load to offset the phase shift and return the PF to near 1. Adding a capacitor across a fan motor with a lagging power factor can cancel out the poor pf.
In many cases one can only partly cancel reduced power factor this way. Eg with electromagnetic ballasted fluorescent strip lights (which have a lagging power factor due to their inductive ballasts), adding a capacitor to create a leading reactive element can cancel out much of the effect of the inductor, but the below 1 PF of the tube itself can't be cancelled so easily. So such fittings, with PF correction capacitor, might end up with a pf of around 0.8.
How to correct PF
- Inductive lagging load: add the right sized capacitor in parallel with the load. If the load can't be relied on to discharge the cap when unplugged, also add a bleeder resistor across the cap.
- Capacitive leading load: in principle one can add a suitable inductor in parallel with the load, but its rare that capacitive loads need compensation, as total house/factory loads are normally lagging, and any capacitive load serves to correct this to some degree.
- Rectifier capacitor load: These can be corrected with either active electronic circuitry or use of relatively large passive components. Both require electronics expertise and are outside the scope of DIY. They're also just about never worth doing.
Note that components used for PFC need to be calculated correctly. Do not just hook up whatever's in the junk box.
Does a low power factor mean I am using more electricity?
Yes and no. LPF does mean drawing more current that you would with a high PF, but no more power is consumed. In a domestic situation a poor power factor does not result in any increased electricity cost.
Low power factors reduce distribution efficiency in the grid slightly, and in some situations can even result in the mains supply waveform getting misshapen - so power supply companies tend to charge big industrial users if they don't control their power factors.
If you want an analogy, imagine riding a bike up hill. You stick a certain amount of push into the pedals to keep it moving overcoming resistance, and more to add the energy you are acquiring by climbing the hill. Imagine someone attaching a big spring to one pedal and the seat post, such that every time you push the right pedal down you also need to stretch the spring. As you can imagine this will take more "push" from you to keep riding. However that extra push is only required on the right pedal. When you push the left pedal you have the energy stored in the spring pulling up on the right pedal and hence working for you. So the result is the bike is harder to ride, but the total energy required to get up the hill is actually the same. This is similar to the effect of having a poor power factor as a result of large reactive elements in the load - the load still dissipates the same amount of energy, but it is harder to drive (i.e. needs more peak current flow).
Fluorescent lights
Most of the time power factor doesn't much matter with fluorescent lighting. But a power factor of eg 0.65 means a light takes 50% more current than if PFCed, and this can run into problems if you've got a large enough quantity of lighting on a circuit to take it over its current rating. Such a situation isn't normally found in houses, but is common in commercial premises.
Electromagnetic ballast
These basic ballasts nearly always flicker and flash when switched on. You can get them in HPF & LPF versions, with PFC capacitor or without.
LPF ballasts are converted to HPF by adding a capacitor across the mains feed. LPF (uncorrected) ballasts cause switches to arc, this may be reduced by adding a small snubber (a 0.1uF capacitor and a 100ohm resistor in series) in parallel with the fitting.
Electronic
Its impractical to add DIY PFC to electronic ballast fluorescent lights. New electronic ballasts over 25w already have PFC.
Generators
Generators are rated by VA rather than power in watts. So a 1kW 0.8pf drill consumes 1.25kVA under load, and the generator needs to supply this.
Connecting a suitable capacitor would allow the above tool to run on some generators that couldn't quite run it without PFC.
Use of tools on generators is more complex than this, as
- many tools also consume well above run current during startup.
- invertor and non-electronic generators behave quite differently with overcurrents, the latter handling them much better.
What about this device that claims to save money?
For industrial users of electricity, PFC can and does save them money. This has led to some makers of gadgets and gizmos to promote them to domestic customers for the same reason. Alas, PFC alone is unlikely to save you anything in electricity, since the standard UK electric meters only measure the real power used, and ignore reactive currents that may also be drawn from (and returned to!) the supply.
See also
- For a very comprehensive explanation of this topic, I recommend this site.
- Category: Electrical
- Category: Appliances
- Wikipedia article